Previously I have used sage on Ubuntu Karmic and loved it.
Just now there is no official Debian or Ubuntu package for sage, and so installing it on my new system (Debian Squeeze) gave me a choice:
- Install the prebuilt binary package that sage themselves provide
- Download the source and issue 'make' on my own machine.
In particular if you are new to sage then the prebuilt binary packages are the 'no hassle' way of getting up and running.
If you just want to see what sage is about, then the live cd, is an excellent way to try things out (no change to your system at all)
Compiling and having sage 'self check':
Summary: make test
Note: I work on GNU/Linux and so my instructions are particular to that platform. Seek out the install guides at sagemath.org if you want help with another platform.
Download the latest .tar file from a mirror listed here.
( My .tar was around 300MB and I checked its md5sum matched against the site )
Untar into /usr/local/ or /opt/local/ or your home directory, as you prefer
( I will use /opt/local for this article )
Have a quick look at the readme file at /opt/local/sage-4.5.3/README.txt
Follow the install guide at sagemath.org in conjunction with this article.
I mentioned about getting sage to 'self check', and what I meant by that, was running the inbuilt mathematical tests that come with sage.
Glancing at README.txt you might be thinking of setting SAGE_CHECK="yes", however this is a different 'self check'*
( *Sage is made up of a number of .spkg files and SAGE_CHECK="yes" will initiate integrity checks on those .spkg files and checks for compatibility with your system )
Running make test initiates a two stage process:
- The build
- mathematical test suite
When you are all done then you might want to issue the following command:
chown -R someuser:root /opt/local/sage-4.5.3/
( replace
someuser with the the username you normally log in with )*** End of main article. ***
( The next section is for those interested in lower level details of sagemath source and .spkg testing in particular )
Bundling python within an application and compatibility:
Sage does not use Python that already existed on your system, and instead, bundles Python 2.6.4 to support all sage applications.
This is a perfectly valid approach* but does freeze in time, that bundled Python, against a moving target (your system and upgrades)
( *as a Debian user I would really like a version of sage that integrates more fully with optimised libraries debian itself took the trouble to install. This is not currently the case and I understand some of the why and why not involved. )
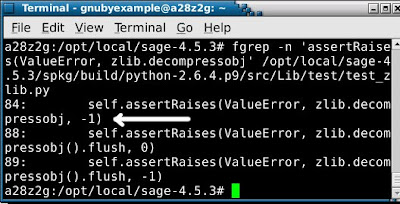
In particular Python 2.6.4 bundled in sage 4.5.3 is probably missing a patch to the file test_zlib.py
Unpatched (as supplied by sagemath.org) my output using SAGE_CHECK="yes" was:
test test_zlib failed -- Traceback (most recent call last):
File "/opt/local/sage-4.5.3/spkg/build/python-2.6.4.p9/src/Lib/test/test_zlib.py", line 84, in test_baddecompressobj
self.assertRaises(ValueError, zlib.decompressobj, 0)
AssertionError: ValueError not raised
322 tests OK.
3 tests failed:
test_distutils test_httpservers test_zlib
...but then applying the patch with a manual edit to the file test_zlib.py
...sees test_zlib outcome being different as shown:
test_zlib
323 tests OK.
2 tests failed:
test_distutils test_httpservers
When the next version of sage (4.6) is officially released, hopefully it will include Python 2.6.5 or newer, so as to have that patch already applied.
Links and reference:
- bugs.python.org issue 8193
- issue 8193 patch follow up in svn - revision=79850
- issue 8193 patch follow up in svn - revision=79850 python
- ask.sagemath.org (Great place to ask an expert)

Attempting a quick linear algebra test, had me working out the differences, in how to define matrices, between different open source mathematics packages.
ReplyDeleteSage:
A=matrix([[0,-2,0],[1,3,0],[0,-6,-1]]);
A*A
Gap:
A:=[[0,-2,0],[1,3,0],[0,-6,-1]];
Display(A^2);
Maxima:
A : matrix([0,-2,0],[1,3,0],[0,-6,-1]);
A^^2;
Note: A . A will do just as good as A^^2 in maxima
in this particular case.
( Do test out the operator is right for your purpose if you are planning more complicated examples. )
If you are really interested in working with matrices in sage, then the first column of this syntax comparison, might prove useful:
http://hyperpolyglot.wikidot.com/math#matrices