- Sage uses Objects to represent mathematical constructs
- Sage is written in Python
two_to_ten=2^10 a_to_power=11^two_to_ten len(str(a_to_power))
Answer: 1067
There are 1067 digits in the number formed when 11 is raised to 1024
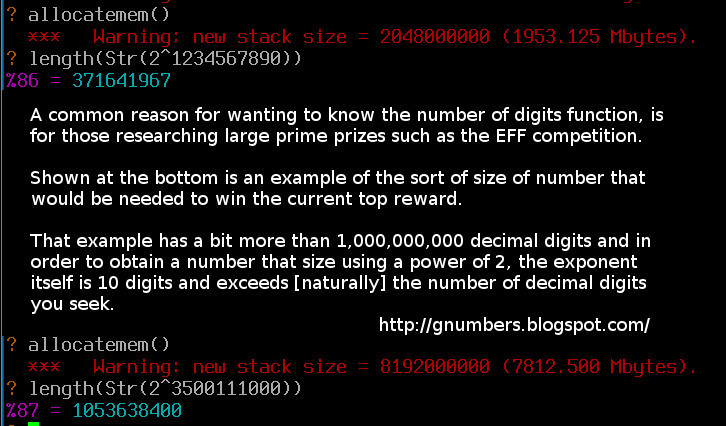
Pari/GP and number of digits:
In Pari/GP the length() function can be used in a similar way to len() in Sage. In Pari try length(Str(11^1024))
You can still access Pari/GP directly through sage.
Try this in Sagemath:
gp("length(Str(11^1024))")The very large - two examples using Pari:
( click on the image above for optimal font sizing )
Notes and further reading:
You can check the 11^1024 digit count yourself by following this wolfram alpha link:http://www.wolframalpha.com/input/?i=11%5E1024
Python note: Although sage allow you to use ^ to indicate raising to power, when writing in Python directly you should use the correct ** operator.
Pari/GP is designed particular for number theory, and does not have a real need to store mathematical constructs as api friendly Objects [by default] in the same way as Sage does.